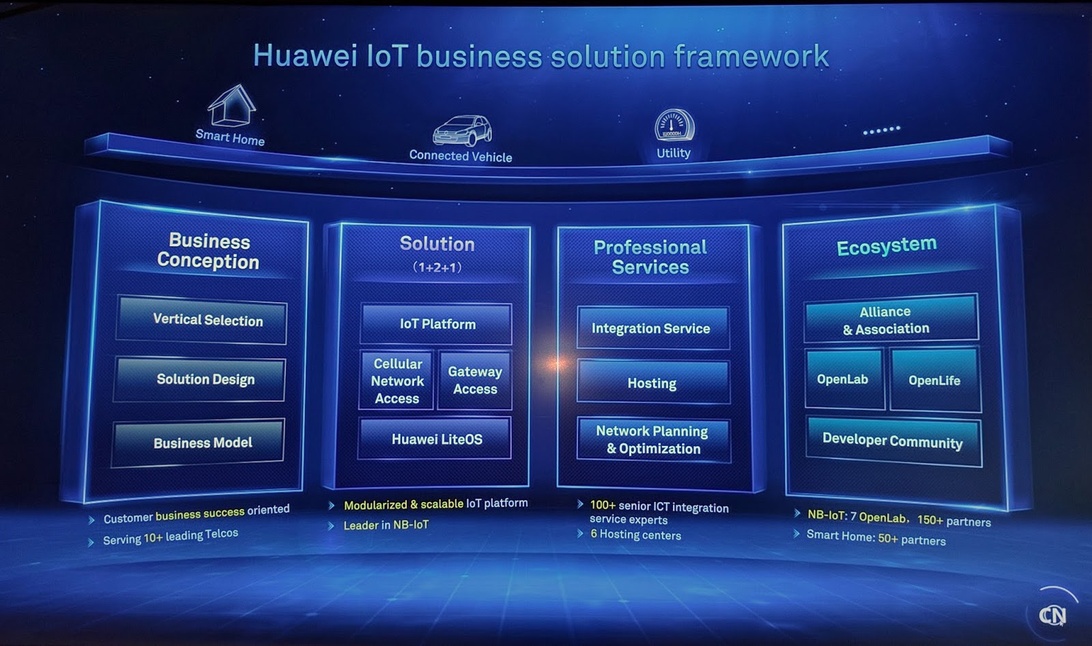
Kuidas asjade internet (IoT) mõjutab Eesti ettevõtete konkurentsivõimet
Asjade internet ehk IoT (Internet of Things) ei ole enam pelgalt tulevikumuusika, vaid käegakatsutav reaalsus, mis kujundab ümber ärimaastikku nii globaalselt kui ka Eestis. See tehnoloogiline revolutsioon, kus seadmed suhtlevad





